Introduction

Figure 1 Merope, who wed the King of Corinth, pictured here gazing skyward at the Pleiades star cluster where her six sisters keep shining eternally after all marrying immortal gods.

The mythology offers three possible explanations as to why only six of the stars in the Pleiades are easily visible to the unaided eye. One of these tales depicts Merope (meaning "mortal") as the "lost Pleiad" masking her face in shame for marrying a mortal, hence her elusive appearance.

Equally elusive is something resembling a bright star visible for a short while on a section of mountain known as the "Seven Sisters", behind my hometown, Wellington. The resemblance continues, involving the death of a mortal.

Although numerous old-Wellingtonians can tell you the story behind the "Hawekwa Mirror", very few have actually seen it shine due to a number of factors. From any particular location it is only visible twice a year for about a week during which it gradually gets brighter before fading back to invisibility. During this maximum it is visible to the naked eye for about 10 minutes but only gets really bright for a few minutes if you catch it during its peak, putting up quite a show to those who happen to be looking at the mountain at this time. As with astronomical observations, visibility is easily impaired by afternoon cloud, either on the mountain or on the opposite sunset horizon.

Factors counting a little in favour of your chances to see it, is that its bi-annual visibility spells traverses the most densely populated parts of Wellington that have a good view of the mountain. Each visibility "season" lasts about 3 months, as the "beam" slowly sweeps across town, corresponding to the daily shift in the sunset position on the horizon. It gets about as bright as the total brilliance of the full moon, concentrated into a single point source.

Most of the above facts about the visibility pattern of the sun's reflection off a granite memorial stone, mounted on the Hawekwa crags behind Wellington, have not been known until recently when I took an intense interest in the elusive "mirror", took some measurements, made predictions by applying some astronomical knowledge and confirmed this by observation.

Folklore

Piet Hugo

The origins of this story goes back to 19 November 1959 when two local boys, Piet Hugo from the farm Hexberg and Frans Ferreira, the only child of the then police chief of Wellington, during their university vacation, set off one Thursday morning to climb the Hawekwas. Frans's beloved Doberman went along and as the party went through the farm Patatskloof, the then owner, Sarel van der Merwe warned them about the wisdom of taking a dog to the mountain. Frans replied that his dog was used to climbing but Sarel's prediction soon came true when the dog got stuck on a narrow ledge high up on a cliff. In an attempt to lift his dog to safety, Frans lost his balance and fell to his death. Although his heroic deed saved his dog's life, story has it that the dog later mourned itself to death.

Figure 2 The author (right) and his son, Jaco-Chris pictured at the plaque with the Afrikaans inscription: IN MEMORY OF FRANS FERREIRA WHO HAD A FATAL ACCIDENT ON THIS MOUNTAIN ON 19 NOVEMBER 1959. ALWAYS BE READY. The dark colour of the granite can be seen here.

Needless to say, the Ferreira's were devastated by the tragic death of their only child and decided to erect a headstone, cemented to the rock-face lower down on the mountain (Fig 2 and inset Fig 3). It is unclear if it was intentional or not, but this stone, being made of highly polished granite, very effectively reflects the light of the setting sun, sweeping across the full width of the town of Wellington. In fact, since most people cannot believe that an almost black stone can produce such a bright reflection, a fairly general story developed stating that a real mirror was put next to the plaque to produce the light. The story even goes further, saying that occasionally this mirror gets disturbed by baboons or overgrown with vegetation which needs to be put right from time to time.

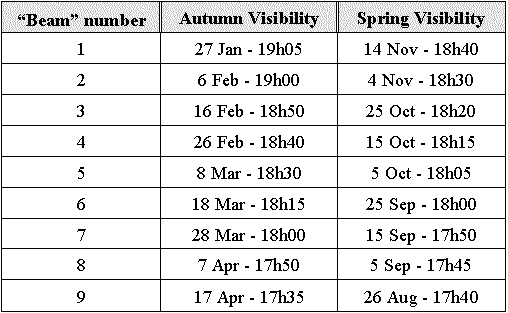
However, on a recent outing to the site no traces of a real mirror could be found, although we did encounter a troop of baboons fleeing right past the monument as we approached. A bigger problem for disturbing a real mirror that I see is the strong winds that can blow up there, ruining any chances of a repeatable reflection. No interfering vegetation can grow near it either since the stone is surrounded by solid rock.

No relationship between the visibility periods I identified (Table 1) and the date of Frans's accident is obvious either, challenging the credibility of claims that the placement of the stone was intentional.

Seeing is believing

I first heard the story of the Hawekwa "mirror" from Jacques Retief, incidentally also born and bred on a subdivision of the original Hexberg farm on the outskirts of Wellington. I was immediately interested and asked him to keep an eye out for it for me. As soon as he spotted it again he invited us over and we happen to catch it close to its maximum. I was amazed by how bright it got for a few minutes which made me realise how the legend of a real mirror could have originated.

I was so intrigued by this phenomena that I immediately wanted to find out more about its dynamics and the possibility of it being visible from my house, a few kilometres south of Hexberg. A quick mental visualisation suggested that it would. Subsequent detailed calculations, considering the actual shift of the sunset position, confirmed this. Local conditions close to the plaque, like obscuring rocks, vegetation, etc. were still unknown at that time but later found not to be a problem.

Figure 3 A picture of the reflection taken at18H58 on 4 February 2002 from close to the Bovlei wine cellar on the Bains Kloof road. The inset picture shows Callie van der Merwe unveiling the stone at the time of its opening ceremony and memorial service.

Finding my bearings

The very next night I was back at Hexberg, this time armed with more than just binoculars. I had since worked out that a lot of the geometry of the "mirror" could be calculated by simply taking a bearing to it. I therefore set up my satellite tracking mount to do just that. This system consists of a 20x80 monocular on an Altitude/Azimuth mount, fitted with setting circles. A vital aid to setting up and aiming this mount, is an old laptop computer running a simple DOS program, ASTRO (downloadable from my website - http://www.saao.ac.za/~wpk/) that I wrote several years ago. ASTRO uses the laptop's internal clock to continuously calculate the position of a celestial object in real time.

Once the mount was orientated on the sun, the monocular was simply pointed at the "mirror" and its bearing read off the setting circles. From Hexberg this was found to be Az 134.3° and Alt 6°. At the instant we observed maximum brightness (19h07 on 26 January) ASTRO gives the position of sun as Az 253°, Alt 8° as seen from Wellington. By making ASTRO step in time, it was found that the sun would also be in this position on 15 November @ 18h39 every year, on its way back to its winter turning point.

In order to determine when I would be able to see the reflection from my house, I also took a bearing from there. This proved not to be that easy to do while it is not reflecting. The biggest problem was finding the monument site because the mountain looks somewhat different from my house compared to from Hexberg. Once I managed to take a picture of the reflection (Fig 3) I could use this photograph as a "finding chart" to guide me to it. To verify that I'm looking at the right spot, I pointed my 9-inch Newtonian telescope at the mountain. I was quite surprised by how clearly visible the plaque was in the telescope (Fig 4). In fact, at 175 power, with the correct lighting and at moments of good seeing, one could actually make out that there is an inscription but was obviously unable to read it.

From my house, the bearing to the stone was measured as Az 113°, Alt 6.7° with reflections calculated to occur on 18 March @ 18h54 and again on 25 September @ 18h00.

Figure 4 A sequence of images grabbed from footage taken from my house on 28 September 2003, three days after predicted maximum, using my 9-inch telescope fitted with a CCD surveillance camera. As can be seen from the fuzzy shadows in the first two pictures, the sun was unfortunately partly obscured by thin cloud initially. Despite this, the "mirror" still put on a good show. LEFT: The rectangular shape of the plaque was very noticeable about ten minutes before maximum. MIDDLE: At maximum, the brilliance of the reflection caused blooming of the CCD pixels and some scattering of light in the telescope optics. RIGHT: Half an hour later the cloud had mostly disappeared but the show was over with the granite stone blending back to near invisibility into the surrounding rock. (Click here for an animation (1.5MByte) spanning 17h44 to 18h22)

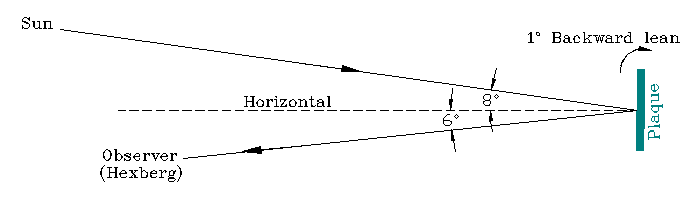
Working out the geometry

Using a 1 : 50 000 map, the line-of-sight distance from my house was estimated at 8km. This map was not very helpful in determining the geometry since it was difficult to determine the exact position of the monument site on the map, mainly because of the very steep contours.

To work out the geometry, I separated the problem into its two components by investigating the plan and side views separately.

The side view is very simple (Fig 5) suggesting that the headstone is tilted back by one degree from the vertical. This result initially surprised me because, judging by the pictures taken at the memorial service and unveiling ceremony (inset, Fig 3) it looks like the stone should lean back more. Measuring this angle was thus specifically done during our expedition to it and found to agree perfectly with the calculation.

Figure 5 A side view of the geometry of the reflection as seen from Hexberg, yielding the 1° lean-back angle of the stone. This value agreed with a subsequent on-site measurement.

Again, by applying the plane mirror reflection law, considering the plan view, the Azimuth of the stone's reflecting surface could easily be determined by both calculation and geometry (Fig 6) without the exact distance to the "mirror" being known. Drawing this to scale, puts the azimuth of the reflecting surface at 193.66° as shown. From this, a ray-trace using the measured bearing from my house yielded the azimuth of the sun when producing a reflection for me. Using ASTRO again, the corresponding dates and times could be determined.

Figure 6 A plan view showing the geometry of the reflections as seen from Hexberg and my house respectively. This was used as a basis for producing Fig 7.

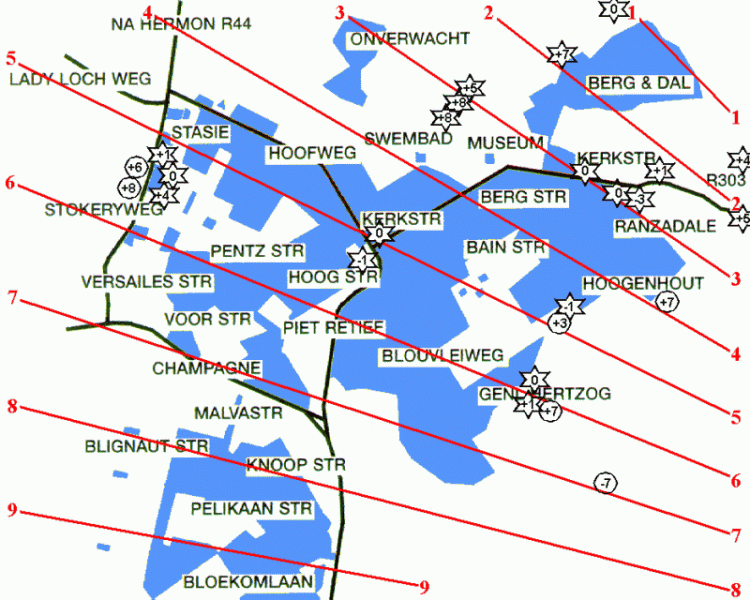
By simply constructing lines at the correct Azimuth angles from Hexberg and my house on a detailed street-map (similar to figure 7 but with much more detail), proved to be a very simple, yet effective way of visualising the problem. Lines at the measured Azimuth angles, representing the reflections from Hexberg ("beam" 1) and my house ("beam" 6) to the position of the stone were first drawn in on the map. Using ASTRO again, the Azimuth of the sun was calculated at 10-day intervals and corresponding reflection lines drawn in on the map. This map was then used as a basis for doing the observations.

Observations

Table 1 Estimated visibility dates in 10-day intervals and times to the nearest 5 minutes, corresponding to the numbered lines or "beams" on the Wellington map, Fig 7. The two visibility "seasons" are apparent.

Since the stone is mounted only 1° off the vertical, the simplified plan view, ignoring this, was found to be accurate enough for observational purposes. Some uncertainty is introduced anyway by factors such as Wellington stretching over many hills and valleys, the proximity of one's viewing position to the mountain affecting the altitude angle, etc. Further simplification was therefore done by calculating with the sun at a fixed altitude of 8° and found to be accurate enough for observational purposes.

To test my predictions, I followed the beam over a period of two months until it got too early for me getting off work. A few more observations over weekends finally totalled 28 points spread over a wide area of Wellington, some spanning a number of days either side of the predicted ideal dates (Fig 7) checking on the visibility window.

Like observing astronomical objects, making use of binoculars greatly increases visibility, easily extending the reflection becoming visible at least 10 minutes before and after the naked eye visibility spell and a number of days either side of the visibility window for a particular location.

I also placed an article in a local newspaper, including Fig 3, sketching the historical background and listing my predictions with a request for observations. Unfortunately, no real useful data was obtained from this. However, some awareness had been generated since I did see one instance of people busy looking at the mountain using binoculars with the newspaper at hand.

A few phone calls resulted, mostly on personal accounts and details of the events surrounding the accident. One very interesting call was from Frans's stepbrother, a boy from the local children's home who was subsequently adopted by the Ferreira's after Frans's death. He unfortunately knew very little since the tragedy was a very sensitive issue for his stepparents who hardly ever mentioned the tragic story.

Figure 7 A simplified map of Wellington with numbered "beams" of visibility of the reflection, corresponding to the dates and times in Table 1. Also shown are some of my observations, depicting successful ones as a star symbol and circled numbers indicating no naked eye reflection was seen, despite conditions being ideal. The numbers inside the symbols indicate the difference in days between the calculated and observed dates. Negative numbers indicate an attempted observation before the predicted date and positive numbers the number of days observed after the prediction.

How bright?

I considered ways of doing photometry, to try and determine the brightness of the reflection but no practical ways could be devised of doing this against the sunlit background of the mountain, constantly changing brightness as the sun sets.

To determine the brightness theoretically, I turned to the proven methods devised by the satellite tracking community. Similar situations occur when sunlight gets reflected off flat surfaces on satellites. The most famous example is perhaps the Iridium satellites capable of producing very predictable "flashes" off their highly reflective door-sized antennae, capable of reaching a brightness of magnitude -8. The solar panels on the Hubble Space Telescope and the International Space Station, to name but a few, also regularly produce spectacular glints.

Studying and analysing these reflections from satellites has been fully characterised by the amateur tracking community and in particular Tony Beresford from Australia who's help was greatly appreciated here. Satellite reflection brightness's are easily measured by comparison to the background stars. The geometry of the satellite orbits are well know making it easy to calculate the distance to the observer, the sun phase angle, etc. Data on the exact sizes of the antennae and solar panels is freely available for unclassified payloads. It is therefore no surprise that predicting satellite reflection brightness's has been refined to a fine art.

These calculations are based on the fact that a perfect mirror of 1 square meter at 1000km range at near zero phase angle gives a specular reflection of magnitude -7. The effect of distance is then compensated for by the inverse square law and the reduction in brightness by the percentage reflection compared to a perfect mirror, taking into account the size of the reflecting area.

The brightness calculation depends a lot on the specular reflectivity of polished granite. No exact value for this could be found, so an estimate had to suffice. Taking into account that solar panels are generally 12% reflective in the visible and that the granite surface has been subjected to almost 45 years of weathering, a value of 10% was deemed reasonable. The plaque is about 400 x 400mm in size and 8 km away.

Using the above methods the brightness was calculated as follows:

Compared to a perfect mirror of 1 m² at 1000km producing brightness of magnitude -7
      The reflection area is 0.16 m². Magnitude of this area at 1000km = -7 + 2 = -5
      At 10% reflectivity the brightness drops 2.5 magnitudes, thus -5 + 2.5 = -2.5
      At 8km range, brightness goes up 125x125 times = 2 x -5.25 = -10.5 magnitudes
      Resulting estimated brightness = magnitude -13.

Readers will recognise this being just slightly brighter than the full moon. Taking into consideration that the moon spans about ½ degree, the reflection of the plaque is a point source, thus about equivalent to the full moon's light concentrated into a single point.

Conclusion

The brightness value seems reasonable considering what have been observed but difficult to compare because of the difference in conditions observing the moon against the sky compared to the tiny reflection against the backdrop of the mountain, lit by the setting sun, still 8° above the horizon.

My visibility predictions, confirmed by observation is accurate to within about a week and ±5 minutes in time, enough to use as a guide to find and track the reflection pattern as it traverses the hills and valleys of the town of Wellington or to know when to expect it to shine for your location.

My efforts has hopefully shone some light (pun intended!) on some of the folklore that developed over time, mainly as a result of poor knowledge and a lack of understanding of the whole phenomena.

As it has done for the past 40-odd years, the reflection of the Hawekwa mirror is likely to continue, bi-annually, bi-directionally, sweeping the town of Wellington for generations to come. Through the memory of Frans Ferreira, it will keep reminding us of the tragic events of 19 November 1959 while blazing out the eternal warning: "ALWAYS BE READY"!

Ds. Ries (met die Bybel) het 'n kort diens gelewer - agter sy rug sit Mnr. Joubert (S.J.) Cillie en net voor Ds. Ries kan Lorraine Cillie gesien word. Teen die rots, agter leun Sarel van der Merwe op sy regterhand - by sy regterskouer steek Guillaume Marais se gesig uit. Heel regs staan Callie van der Merwe. Die persoon agter regs (met die bril in die hempsak) is Mnr. Piet Conradie van die Paarl Bergklub wat Frans se liggam herwin het. Die jong seun wat voor Ds. Ries sit is Piet Hugo wat saam met Frans geklim het.

Sersant Ferreira (regs), die vader van Frans en Ds. Ries (middel) en kyk toe terwyl oom Callie (C.A.) van der Merwe die steen onthul.